Memory requirement estimation is an important issue in the development of embedded systems, since memory directly influences performance, cost and power consumption. So it is crucial to have tools that automatically compute accurate estimates of the memory requirements of programs to better control the development process and avoid some catastrophic execution exceptions. We propose an original approach based on the theory of Bernstein expansion allowing the resolution of many important memory issues that are expressed as the problem of maximizing a parametric polynomial defined over a parametric convex domain.

Bernstein expansion allows bounding the range of a multivariate polynomial considered over a box. Numerical applications of this theory have been proposed to the resolution of system of strict polynomial inequalities. It has been shown that Bernstein expansion is generally more accurate than classic interval methods. Moreover, Stahl has shown that for sufficiently small boxes, the exact range is obtained. 

Bernstein polynomials are particular polynomials that form a basis for the space of polynomials. Hence any polynomial can be expressed into this basis through coefficients, the Bernstein coefficients, that have interesting properties and that can be computed through a direct formula. Due to the Bernstein convex hull property, the value of the polynomial is then bounded by the values of the minimum and maximum Bernstein coefficients. The direct formula allows symbolic computation of these Bernstein coefficients giving a supplementary interest to the use of this theory.

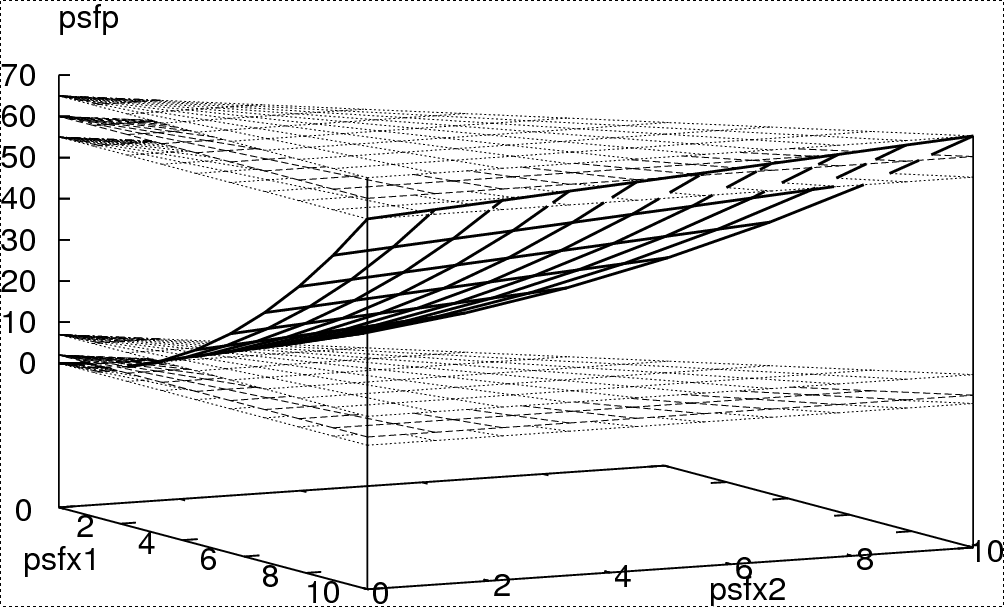
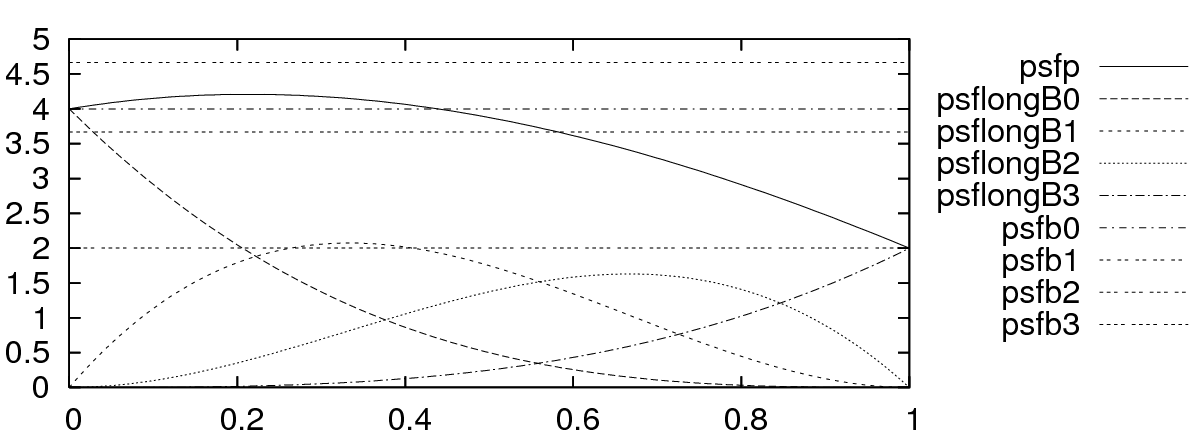
Our symbolic Bernstein and polynomial maximization approach has been implemented by Federico Fernandez and Sven Verdoolaege. It is freely available and can be dowloaded here : bernstein-0.01.tar.gz. Before installing it, you need also to install the GNU Multiple Precision Arithmetic Library, the polyhedral library PolyLib and ginac. Explanations and examples can be found in the software package. Notice that this bernstein library has also been included in the barvinok library since release 0.22.

Philippe Clauss, Federico Javier Fernandez, Diego Gabervetsky and Sven Verdoolaege. Symbolic Polynomial Maximization over Convex Sets and its Application to Memory Requirement Estimation, Research report ICPS number 06-04, Université Louis Pasteur, October 2006.

Ph. Clauss and I. Tchoupaeva A Symbolic Approach To Bernstein Expansion (in russian), in Programmirovanie (Programming and Computer Software), Vol. 30, No. 3, 2004, Russian Academy of Sciences, Nauka, Moscow.

Ph. Clauss and Irina Tchoupaeva, A Symbolic Approach to Bernstein Expansion for Program Analysis and Optimization, 13th International Conference on Compiler Construction, CC 2004, LNCS 2985, pp 120-133, Springer, April 2004, Barcelona, Spain.