Il s'agit d'implémenter 2 stratègies de réduction des expressions du lambda-calcul pur:
- la stratégie NOR jusqu'à obtenir une Forme Normale (évaluation paresseuse)
- la stratégie AOR jusqu'à obtenir une Forme Normale Faible (évaluation affairée).
- Définir un type CAML qui représente les expressions du lambda-calcul pur
- Ecrire, en utilisant ce type, quelques fonctions CAML qui construisent des lambda-expressions simples comme:
x.x ou
x.
y.x ou
x.
y.(x y) ou encore
x.(x x)
- Ecrire une fonction qui, dans une expression exp, remplace toutes les occurrences libres d'une variable y par une autre expression exp1
- Ecrire une fonction qui applique la règle de béta-conversion
- Ecrire une fonction qui réduit une expression à une FNF.
On peut imaginer 2 façons de représenter un graphe orienté:
- par une liste d'arcs entre 2 sommets
- par une liste de sommets et une fonction qui à un sommet (origine) associe une liste de sommets (destination)
Il s'agit de:
I) définir un type pour chacune des réprésentations
et écrire les fonctions permettant de changer de représentation
II) pour chacune des 2 représentations, écrire une fonction qui compte le nombre de chemins entre 2 sommets.
III) généraliser et trouver 2 représentations pour des graphes où chaque arc est affecté d'une longueur,
et pour chacune de ces 2 représentations,
écrire une fonction qui trouve le plus court chemin entre 2 sommets.
Il s'agit de généraliser les fonctions sur les arbres binaires (avec au plus 2 sous-arbres) aux arbres quelconques (avec un nombre quelconque de sous-arbres).
Pour cela, définir un type pour les arbres quelconques, puis:
I) Définir les fonctions permettant de décompter:
- le nombre de feuilles
- le nombre de noeuds
- le nombre d'arcs
II) Définir les fonctions qui retournent la liste des sommets rencontrés lors d'un parcours:
- préfixé (en profondeur d'abord)
- infixé
- postfixé
- en largeur d'abord
Le codage de Huffman permet de comprimer un fichier texte.
La compression de données est utilisée pour augmenter les capacités de stockage en mémoire ou les vitesses de transmission.
La compression est composée d'un encodage et d'un décodage. Il faudra donc écrire ces 2 fonctions.
Voir ici ou ici pour une description détaillée du codage de Huffman.
Il s'agit d'écrire certaines fonctions sur des arbres qui peuvent comporter un nombre infini de noeud et dont le type est donné ci-dessous:
type ('a,'b) ftree = Null | Node of 'a * ('b -> ('a,'b) ftree);;Un arbre infini est:
- soit vide (Null)
- soit un noeud avec:
. une valeur de type 'a
Ecrire une fonction maptree qui applique une fonction sur toutes les valeurs d'un arbre infini (de façon similaire à la fonction map pour les listes).
. un nombre quelconque de sous-arbres, chacun étant étiqueté par une valeur de type 'b
(on choisit d'utiliser une fonction de type 'b -> ('a,'b) ftree plutôt qu'une liste de type ('b * ('a,'b) ftree) list)
Ecrire les fonctions permettant de définir les arbres dessinés ci-dessous (étant donnée une fonction f):
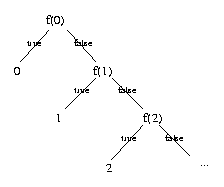
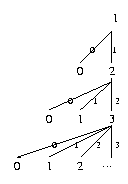
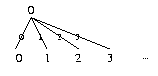
Il s'agit d'implémenter un système de réécriture càd un système permettant d'appliquer de façon automatique des régles de réécriture.
Définitions prélimnaires:
Un terme est construit à partir de constantes, de variables et d'opérateurs.
Un terme t1 filtre un terme sans variable t2 ssi il existe une substitution s telle que s.t1 = t2.
Une règle de réécriture s'écrit t1 -> t2 où t1 et t2 sont des termes avec variables.
Soit t un terme sans variable. La règle t1 -> t2 s'applique à t si t1 filtre un sous-terme, disons tr, de t.
Alors, le résultat de l'application de la règle est t dans lequel tr a été remplacé par s.t2, où s est la substitution telle que s.t1 = tr.
Exemple:
La règle x * (y + z) -> x * y + x * z appliquée au terme b + a * (b + c) * d + a * c
donne le terme b + (a * b + a * c) * d + a * c.
Il s'agit de:
- Représenter termes, règles de réécriture, et substitutions
- Ecrire une fonction qui:
- filtre un terme par un autre : le résultat est une substitution (ou une exception si le filtrage échoue).
- Tester sur l'exemple suivant:
- applique une règle sur un terme (sans variable) : le résultat est un terme sans variable (ou une exception si la règle ne s'applique pas).
- applique une liste de règles sur un terme : le résultat est le terme obtenu en appliquant la première règle de la liste qui s'applique.
- applique une liste de règles sur un terme jusqu'à ce qu'aucune des règles de la liste ne s'applique plus.
Règles:
1 * x -> x (1/x) * x -> 1 (x * y) * z -> x * (y * z) (1/x) * (x * y) -> y x * 1 -> x (1/1) -> 1 (1/(1/x)) -> x x * ((1/x) * y) -> y (1/(x * y)) -> (1/x) * (1/y)Terme: (1/((1/a) * (1/b)))
Il s'agit d'implémenter un petit langage fonctionnel à évaluation paresseuse. Il s'agit donc d'écrire un analyseur syntaxique et un interpréteur pour ce langage. Pour écrire l'analyseur syntaxique, on se servira de camlyacc (cf. documentation sur ocaml).
Un programme dans ce langage est une suite de définitions de fonctions de la forme suivante:suivie d'une expression à évaluer. La syntaxe d'une expression est la suivante (en BNF):
Soit<nom_fonction>(<var1>,<var2>,...,<varn>) =<expr>.
Exemple: dans ce langage, on peut écrire le programme suivant:
<expr> ::= <var> (variable) | <nom_fonction> (<expr1>,<expr2>,...,<exprn>)(application) | 0|1|2| ...(entiers) | vrai|faux(booléens) | si<expr>alors<expr>sinon<expr>(conditionnelle) | <expr> ( +|-|*|/|<=|=>|<|>|=) <expr>(opérateurs binaires) | ( +|-) <expr>(opérateurs unaires) | (<expr>)(parenthèsage) Soit ou_logique(x,y) = si x alors vrai sinon y. ou_logique((75>0),(75/0=75))Ce programme comporte la définition de la fonctionou_logiqueet une expression à évaluer. L'évaluation de cette expression donne le résultatvrai, parce que conformément au procédé d'évaluation paresseuse, l'expression(75/0=75)n'est pas évaluée.