Université Louis Pasteur
LICENCE 2ème année
Mardi 7 Novembre 2006
 
Travaux Pratiques de
Programmation Fonctionnelle
(sujet n°3)



I. Schémas de programme.

(a) Utiliser les schémas :
  • List.fold_left f a [b1; ...; bn]  = f (... (f (f a b1) b2) ...) bn
  • List.fold_right f [a1; ...; an] b = f a1 (f a2 (... (f an b) ...))
    pour définir les fonctions :
  • Concaténation des éléments d'une liste de chaines de caractères. 
        Exemple :     concat_string ["a";"b";"c"] = "abc"
  • Liste des nombres pairs d'une liste de nombres entiers (en préservant l'ordre des éléments dans la liste).
        Exemple :     pairs [2;3;5;7;4] = [2;4]
  • Fonction map vérifiant :
      map f [a1; a2; ...; an] = [f a1; f a2; ...; f an]


(b) Définir les schémas :
  • for_all p [a1; ...; an] = (p a1) & (p a2) & ... & (p an)
  • exists p [a1; ...; an] = (p a1) or (p a2) or ... or (p an)
    où p est un prédicat de type 'a -> bool.
Utiliser ces schémas pour définir une fonction qui détermine si tous les éléments d'une liste d'entiers sont pairs (proposer une solution avec le schéma for_all et une autre avec le schéma exists).
(c) (Cribble d'Erathostène.) Il s'agit d'un algorithme classique pour trouver les nombre premiers inférieurs à n. Erathostène (un contemporain d'Archimède) a imaginé la méthode suivante :

    Créer la liste de tous les nombres entiers de 2 à n :

        [2;3;4;5;6;7;8;9;10;11;12;13;14;15;16;17;18;19;20;21;22;23;24;25; ...]

    Eliminer de la liste tous les multiples du premier nombre (2) :

        [2;3;5;7;9;11;13;15;17;19;21;23;25; ...]

    Eliminer de la liste tous les multiples du nombre suivant (3) :

        [2;3;5;7;11;13;17;19;23;25; ...]

    Eliminer de la liste tous les multiples du nombre suivant (5) :

        [2;3;5;7;11;13;17;19;23; ...]

    etc., jusqu'au dernier nombre de la liste. A la fin, les nombres qui restent sont premiers.

    Ecrire un programme Ocaml qui, étant donné n, calcule la liste des nombres premiers inférieurs à n avec cet algorithme. Utiliser le schéma List.fold_right.


II. Bibliothèque de fonctions.

(a) On se propose ici d'utiliser une librairie de fonctions graphiques créée spécialement pour ce TP. Pour ce faire, télécharger dans votre répertoire les fichiers dessin.cma et dessin.cmi, puis, dans l'interpréteur ocaml, taper les phrases  #load "dessin.cma";; (pour charger le code objet) et open Dessin;; (pour charger l'interface). Cette librairie minimaliste définit un type dessin, dont la définition est cachée, un type couleur = Blanc | Noir | Rouge | Vert | Bleu | Jaune, et un type position = Point of int * int. Elle se compose des 2 fonctions suivantes : 
  • trait : position -> position -> couleur -> dessin -> dessin qui ajoute un segment défini par 2 points au dessin dans la fenêtre. Elle prend en argument 2 points, une couleur et un dessin et retourne un nouveau dessin.
  • fenetre : (dessin -> dessin) -> bool qui affiche un dessin dans la fenêtre graphique. Elle prend en argument une fonction, disons f : dessin -> dessin, qui transforme un dessin (qui a un dessin associe un nouveau dessin en ajoutant des traits). Elle ouvre la fenêtre graphique, applique la fonction f,  attend la frappe d'une touche du clavier pour donner le temps de voir le dessin, ferme la fenêtre graphique et enfin retourne true.  La fenêtre graphique a une taille 800x600 pixels (le coin en bas à gauche a pour coordonnées (0,0) et celui en haut à droite (799,599))
Voici un exemple montrant comment cette librairie peut être utilisée :

let croix d =

    let coinbg = Point (0,0)     in
    let coinhd = Point (799,599) in
    let coinhg = Point (799,0)   in
    let coinbd = Point (0,599)   in

        trait coinbg coinhd Noir (trait coinhg coinbd Noir d);; 
 
fenetre croix;;     (* dessine une croix noire *)


(b) Définir une fonction carre : int -> couleur -> position -> dessin -> dessin qui dessine un carré étant donnés sa taille en pixels, sa couleur et les coordonnées de son coin en bas à gauche.

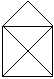
(c) Définir une fonction maison : int -> couleur -> position -> dessin -> dessin qui dessine une petite maison de la forme ci-dessous étant donnés sa taille en pixels, sa couleur et les coordonnées de son coin en bas à gauche.

Petite maison

(d) On souhaite écrire un programme qui simule le mouvement d'une balle qui rebondit contre les 4 murs d'une pièce carrée. La balle sera symbolisée par un petit carré noir de taille 20x20 pixels et pourra prendre l'une des 4 directions définies par les vecteurs (-1,-1), (-1,1), (1,-1) et (1,1). On modélisera l'état courant du système par un triplet (pos,dir,d) avec pos, la position de la balle (le couple des coordonnées du coin en bas à gauche), dir, sa direction (un couple d'entiers) et d, une valeur de type dessin. On utilisera les définitions de type suivantes :

        type direction = Vecteur of int * int;;

        type etat = Triplet of position * direction * dessin;;

  • Ecrire une fonction au_bord : position -> bool qui étant donné la position de la balle retourne true si la balle touche un mur, false sinon.
  • Ecrire une fonction autre_direction : etat -> direction qui étant donné un état courant retourne la nouvelle direction de la balle après qu'elle ait heurté un mur.
  • Ecrire une fonction bouge : etat -> etat qui étant donné un état courant, effectue un déplacement de la balle : la balle avance d'un pas dans sa direction. La fonction renvoie un nouvel etat dans lequel la balle a une nouvelle position et éventuellement une nouvelle direction si elle touche un mur.
  • Ecrire une fonction trajectoire : int -> etat -> etat qui étant donné un entier n, effectue n déplacements consécutifs de la balle. Pour donner le temps d'observer la trajectoire de la balle, on pourra utiliser une fonction frein dont le seul objet est de ralentir le programme.