Programmation Fonctionnelle
(sujet
n°1)
I. Fonctionnement de l'interpréteur.
(a) Lire les informations suivantes :
(b) En utilisant l'interpréteur, évaluer les expressions suivantes (lire la réponse de l'interpréteur) :
(d) Evaluer ces expressions utilisant le mot-clef
II. Décomposition fonctionnelle d'un problème.
(a) Taper les fonctions suivantes (vues en TD) :
(b) Appliquer les fonctions de la question (a) de façon à vérifier les propriétés suivantes :
Soient les points O(0,0), A(cos(-π/4),sin(-π/4)), B(cos(π/2),sin(π/2)) et C(cos(π/8),sin(π/8)). Alors
(d) Appliquer les fonctions de la question (c) de façon à montrer les propriétés suivantes :
(f) (Question facultative) Définir la fonction :
III. Récursivité et complexité.
(a) Taper les fonctions suivantes (vues en TD) :
I. Fonctionnement de l'interpréteur.
(a) Lire les informations suivantes :
L'interpréteur se lance par la commande
ocaml.
L'invite de l'interpréteur est #. Pour sortir de
l'interpréteur faire Ctrl+D. Afin de ne pas perdre
vos programmes, vous pouvez taper vos expressions Ocaml dans un fichier
.ml, par exemple TP1.ml, et les
utiliser ensuite dans l'interpréteur en tapant la directive #use
"TP1.ml";; (attention, ici le #
n'est pas l'invite de l'interpréteur, mais doit être
tapé). Dans un fichier vous pouvez mettre des commentaires entre
(* et *). (b) En utilisant l'interpréteur, évaluer les expressions suivantes (lire la réponse de l'interpréteur) :
1+2*3;;1.0 * 2;;(1 < 2);;int_of_char('a');;"Photo"^"graph";;let pi = 4.0 *. atan 1.0;;let carre x = x *. x;;carre(sin pi) +. carre(cos pi);;
(c) Définir la fonction
carré d'un nombre réel dans un fichier
carre.ml
puis appliquer cette fonction dans l'interpréteur en utilisant
la directive use.function
et la construction let ... in ... :(function x -> 2*x+1) 3;;let x = 3 in 2*x+1;;(function x -> (function y -> x*y)) 2 5;;let x = 2 in let y = 5 in x*y;;let (x,y) = (2,5) in x*y;;
let x = 2 in let y = x+3 in x*y;;(function x -> function y -> function z -> function t -> t) 'x' 'y' 'z' 't'
II. Décomposition fonctionnelle d'un problème.
(a) Taper les fonctions suivantes (vues en TD) :
longueur(longueur d'un segment)
circonference(circonference d'un cercle)
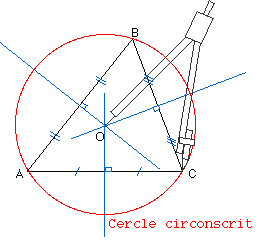
cercle_circonscrit(cercle circonscrit à 3 points)
où une droite est définie
par les coefficients a (pente) et b (ordonnée à
l'origine) de l'équation y = ax+b.

(b) Appliquer les fonctions de la question (a) de façon à vérifier les propriétés suivantes :
Soient les points O(0,0), A(cos(-π/4),sin(-π/4)), B(cos(π/2),sin(π/2)) et C(cos(π/8),sin(π/8)). Alors
- la longueur des segments [O,A], [O,B] et [O,C] est 1.
- la circonférence du cercle circonscrit à A, B et C est 2π.
intersection_vide(test si l'intersection de 2 intervalles est vide)
union_inter(plus petit intervalle contenant 2 intervalles)contigus3(contiguïté de 3 intervalles)
où un
intervalle [a,b] est défini par le couple (a,b) de ses bornes
inférieures (a) et supérieures (b) et en convenant que
l'intervalle est vide si a>b.
(d) Appliquer les fonctions de la question (c) de façon à montrer les propriétés suivantes :
- l'intersection de [2,4] et [1,2] est non vide.
- l'intersection de [4,5] et [1,2] est vide.
- le plus petit intervalle contenant [1,2] et [4,5] est [1,5].
- les intervalles [1,2], [4,5], [2,4] sont contigus.
(e) Reprendre les questions (a) et
(b) en définissant une droite par les 3 coefficients a,b,c de
l'équation ax+by+c=0.
(f) (Question facultative) Définir la fonction :
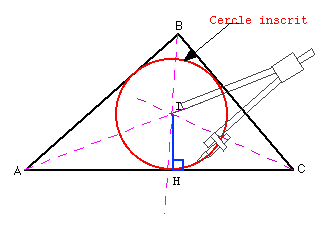
cercle_inscrit(cercle inscrit dans un triangle)

Le cercle inscrit est le cercle tangent aux cotés du triangle.
Son centre I est situé à l'intersection des bissectrices.
Les trois bissectrices sont concourantes en I. Pour trouver le rayon,
il faut tracer la perpendiculaire à l'un des côtés
passant par I. Cette perpendiculaire coupe le côté en un
point H. Le rayon du cercle inscrit est [IH].
(g) Reprendre la question (c) et (d)
en définissant un intervalle (non vide) par le couple (a,b) ou
(b,a) de ses bornes inférieures (a) et supérieures (b).
III. Récursivité et complexité.
(a) Taper les fonctions suivantes (vues en TD) :
puissance(calcul de x^n)
pgcd(plus grand commun diviseur de 2 nombres entiers)
fib(terme de la suite de Fibonacci)premier(test de primalité)
(b) Vérifier que les
définitions récursives de la question (a) sont correctes
sur quelques exemples à choisir.
(c) La directive
#trace
permet de tracer l'exécution d'une fonction. Après que
cette directive a été tapée, tous les appels
à la fonction sont "tracés" : cela signifie qu'à
chaque appel, l'argument et le résultat sont affichés.
Cette directive est intéressante pour analyser le comportement
opérationnel d'une définition récursive. Essayer
cette directive avec la fonction fib en tapant #trace
fib;; puis fib(3);;.