Université Louis Pasteur
LICENCE 1ère année
Mercredi 9 mai 2007
Travaux
Pratiques
Algorithmique et Programmation
(sujet
n°4)
Exercices
1 Dominos
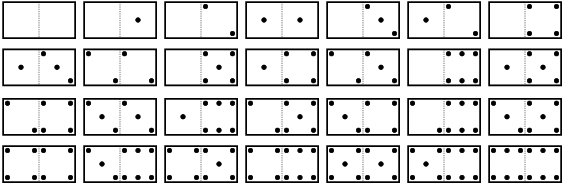
Le jeu des dominos comporte 28 pièces répertoriées
dans la table ci-dessous.
Chaque pièce, appelé domino,
a une forme rectangulaire et est divisé en deux moitiés
blanches marquées de points noirs.
Le nombre de points noirs dans chaque moitié est compris entre 0
et 6
et indique une des 2 valeurs du domino. Un domino est donc
défini par 2 valeurs entre 0 et 6 (par exemple (2-3)). A noter
qu'un domino est réversible (autrement dît, (2-3) et (3-2)
définissent le même domino).
1.1 Type domino
Définir le
type domino des dominos. On utilisera une structure à
2 champs : val_inf et
val_sup tels
que val_inf <= val_sup. Définir les
opérations suivantes :
- cons_domino qui construit un domino à partir de 2
valeurs.
- val_inf qui détermine la plus petite des 2
valeurs d'un domino.
- val_sup qui détermine la plus grande des 2
valeurs d'un domino.
- points_domino qui détermine le nombre total de
points noirs sur un domino donné.
- prem_domino qui, étant donné un entier n,
détermine le premier domino ayant un total de n points
noirs, dans la table ci-dessus (dans cette table, les dominos sont
ordonnés dans le sens de la lecture de gauche à droite et
de haut en bas : le premier est en haut à gauche, le dernier est
en bas à droite).
- suiv_domino qui détermine le domino suivant d'un
domino donné, dans la table ci-dessus.
- compte_domino qui, étant donné un entier n,
compte le nombre de dominos ayant un total de n points noirs.
1.2 Utilisation des dominos
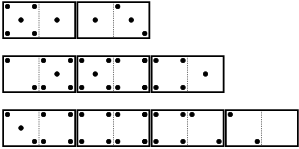
Dans la variante classique du jeu de dominos, on forme des chaînes
linéaires de dominos en réunissant des
moitiés ayant la même valeur. Ci-dessous 3 exemples de
chaînes linéaires avec (de bas en haut) 2, 3 et 4 dominos :
Définir les fonctions suivantes :
- chainable2 qui détermine s'il est possible de
former une chaîne linéaire avec 2 dominos donnés
(ex: c'est possible avec (2-3) et (1-3), impossible avec (2-3) et (1-4))
- chainable3 qui détermine s'il est possible de
former une chaîne linéaire avec 3 dominos donnés
(ex: c'est possible avec (2-3), (2-4) et (1-3), impossible avec (2-3),
(2-4) et (1-2))
Indication : rechercher
parmi les 3 dominos, 2 dominos qui peuvent former un début de
chaîne, si le domino restant ne peut pas être ajouté
à la chaîne, alors aucune chaîne ne peut être
formée avec ces 3 dominos. Attention au cas particulier
où le domino restant a ses 2 valeurs identiques.
2 Intervalles
Définir le type intervalle des intervalles
réels ouverts ] a, b [.
Définir les fonctions correspondantes aux opérations
suivantes sur les intervalles ouverts :
- borne inférieure d'un intervalle,
- borne supérieure d'un intervalle,
- appartenance d'un réel à un intervalle,
- intersection de 2 intervalles,
- milieu d'un intervalle.
3 Ensembles
Définir le type
ensemble des
ensembles dont les éléments sont des entiers. On
utilisera une structure à deux champs
: un entier card égal au cardinal de l'ensemble et un tableau dynamique elementcontenant
les éléments de l'ensemble. Définir
les fonctions correspondantes aux opérations suivantes :
- ensemble vide (la fonction retourne l'ensemble vide),
- appartenance d'un entier à un ensemble (la fonction
retourne un booléen) ( Ex. 2 ∈
{ 1, 2} ),
- cardinal d'un ensemble ( Ex. card({
1, 3 }) = 2 ),
- inclusion d'un ensemble dans un autre (la fonction retourne un
booléen) ( Ex. { 1, 2 } ⊆ {
2, 1, 3 } ),
- union de deux ensembles ( Ex. {
1, 2 } ∪ { 1, 3, 4 } = { 1, 2, 3, 4 } ),
- intersection de deux ensembles ( Ex. { 2, 3, 4 } ∩ { 2, 4, 5 } = { 2, 4 } ),
- différence de deux ensembles ( Ex. { 1, 2, 3, 4 } - { 2, 4 } = { 1, 3 }
).