
Exemples

Exemple 1 : Addition
d'une matrice et de sa transposée

Exemple 2 : Changement
de base
M = align :: V
align =  (i)|(0<=i<=3).(i
mod 2,i/2)
(i)|(0<=i<=3).(i
mod 2,i/2)

Exemple 3 : Routage
W = V  shift
shift
shift =  (i).((i-1)
mod 4)
(i).((i-1)
mod 4)
W = V  spread
spread
spread =  (i)|(0<=i<4).(0)
(i)|(0<=i<4).(0)

Exemple 4 : Réduction
géométrique
Y = merge ;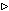 X
X
merge =  (i)|(0<=i<3).(0)
(i)|(0<=i<3).(0)

Exemple 5 : Opération
fonctionnelle
W = inc 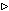 V
V
inc=  (a).(a+3)
(a).(a+3)

Exemple 6 : Sémantique
d'une équation

Exemple 7 : Interprétation
fonctionnelle d'un champ résultat

Exemple 8 : Raffinement
d'un programme
Le programme P2 est raffiné par le programme P3

Exemple 9 : Méthodes
de raffinement
Raffinement par introduction d'un champ intermédiaire
Affaiblissement des pré-équations
Renforcement des post-équations
P5 raffiné par P6
P6: X 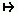 Y
Y
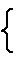 |
vecteur :: Z = X
Y = vecteur :: Z |

Exemple 10 : Construction
d'un programme de multiplication de matrices avec VPEI

Exemple 11 : Transformation
par changement de base
Le programme suivant traduit l'algorithme d'élimination de Gauss
: il résout le système linéaire Ax = b où
A est une matrice nxn et b un vecteur de taille
n. L'algorithme procède pour cela à une triangularisation
de la matrice A, ce à quoi nous nous intéressons ici.
Les champs de données en entrée sont donc la matrice A
et le vecteur B et les champs de données en sortie sont la
matrice triangularisée XN et le vecteur modifié YN.
Le programme Gauss1 fait appel
à des opérations de type diffusion, comme par exemple la
fonction pivot, en choisissant
l'axe k comme direction d'ordonnancement.
Le programme Gauss2 est une
version systolique du programme Gauss1,
obtenu par un nombre fini d'applications successives des règles
de raffinement, définissant ainsi une stratégie bientôt
implantée dans l'environnement de transformation.
Gauss1 : (A,B) 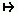 (XN,YN)
(XN,YN)
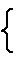 |
A = alignx :: X
B = aligny :: Y
C = el 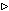 (X /&/ Y /&/ (C
(X /&/ Y /&/ (C  pre)
/&/ (C pre)
/&/ (C  cp) /&/ (C cp) /&/ (C  lp) /&/ (C
lp) /&/ (C  pivot)) pivot))
XN = C  last1
last1
YN = C  last2
last2 |
alignx =  (i,j,k)|(1<=i<=n
& 1<=j<=n & k=0).(i,j)
(i,j,k)|(1<=i<=n
& 1<=j<=n & k=0).(i,j)
aligny =  (i,j,k)|(1<=i<=n
& j=n+1 & k=0).(i)
(i,j,k)|(1<=i<=n
& j=n+1 & k=0).(i)
pre =  (i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(i,j,k-1)
(i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(i,j,k-1)
pivot =  (i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(k,k,k-1)
(i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(k,k,k-1)
cp =  (i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(i,k,k-1)
(i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(i,k,k-1)
lp =  (i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(k,j,k-1)
(i,j,k)|(k<=i<=n
& 1<=j<=n+1 & 0<k).(k,j,k-1)
el = id #  (a;b;c;d).(a-b*c/d)
(a;b;c;d).(a-b*c/d)
last1 =  (i,j,k)|(1<=i<=n
& i<=j<=n & k=i-1).(i,j,k)
(i,j,k)|(1<=i<=n
& i<=j<=n & k=i-1).(i,j,k)
last2 =  (i,j,k)|(1<=i<=n
& j=n+1 & k=i-1).(i,j,k)
(i,j,k)|(1<=i<=n
& j=n+1 & k=i-1).(i,j,k)
Gauss2 : (A,B) 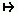 (XN,YN)
(XN,YN)
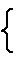 |
A = alignx' :: X
B = aligny' :: Y
C = el 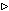 (X /&/ Y /&/ (C
(X /&/ Y /&/ (C  pre')
/&/ (C pre')
/&/ (C  cp') /&/ (C cp') /&/ (C  lp') /&/ (C
lp') /&/ (C  pivot')) pivot'))
XN = C  last1'
last1'
YN = C  last2'
last2' |
alignx' =  (i,j,k)|(1<=i<=n
& 1<=k-i-j<=n & j=1).(i,k-i-j)
(i,j,k)|(1<=i<=n
& 1<=k-i-j<=n & j=1).(i,k-i-j)
aligny' =  (i,j,k)|(1<=i<=n
& k-i-j=n+1 & j=1).(i)
(i,j,k)|(1<=i<=n
& k-i-j=n+1 & j=1).(i)
pre' =  (i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(i,j-1,k-1)
(i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(i,j-1,k-1)
pivot' =  (i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(j,j-1,3*j-1)
(i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(j,j-1,3*j-1)
cp' =  (i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(i,j-1,i+2*j-1)
(i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(i,j-1,i+2*j-1)
lp' =  (i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(j,j-1,j+k-i-1)
(i,j,k)|(j<i<=n
& 2*j+i<k & k-i-j<=n+1 & 1<=j<=n).(j,j-1,j+k-i-1)
el =
id #  (a;b;c;d).(a-b*c/d)
(a;b;c;d).(a-b*c/d)
last1' =  (i,j,k)|(1<=i<=n
& i<=k-i-j<=n & j=i-1).(i,j,k)
(i,j,k)|(1<=i<=n
& i<=k-i-j<=n & j=i-1).(i,j,k)
last2' =  (i,j,k)|(1<=i<=n
& k-i-j=n+1 & j=i-1).(i,j,k)
(i,j,k)|(1<=i<=n
& k-i-j=n+1 & j=i-1).(i,j,k)

Exemple 12 : Simplification
des communications - application au produit matrice-vecteur
Considérons une première version, systolique, de programme
du produit matrice-vecteur, calculant p = A x b, où
b est un vecteur de longueur n. La première phase
de ce calcul, auquel nous nous intéressons ici exclusivement, consiste
a effectuer la multiplication des coefficients.
Dans le programme Matvect1,
le vecteur b est initialement placé sur la diagonale de la
matrice A. A chaque étape indexée par k, on
effectue n produits pii = Ai,i x bi
sur la diagonale. Tous les éléments de A sont ensuite
décalés vers la gauche, et les éléments de
b sont décalés le long de la diagonale, vers le haut
à gauche, les bords étant bouclés toroïdalement.
Au bout de n étapes, on possède l'ensemble des produits
sur le plan (i = j) du cube.
Matvect1 : (M,V) 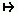 P
P
|
|
A0 = cube :: A0
B0 = cube :: B0
M = aligna :: A0
V = alignb :: B0
A = A0 /&/ (A  left)
left)
B = B0 /&/ (B  upleft)
upleft)
P = prod 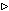 ((A /&/ B)
((A /&/ B)  diag) diag)
|
cube =  (i,j,k)|(0<=i,j,k<n).(i,j,k)
(i,j,k)|(0<=i,j,k<n).(i,j,k)
aligna =  (i,j,k)|(0<=i,j<n
& k=0).(i,j)
(i,j,k)|(0<=i,j<n
& k=0).(i,j)
alignb =  (i,j,k)|(0<=i,j<n
& i=j & k=0).(i)
(i,j,k)|(0<=i,j<n
& i=j & k=0).(i)
left =  (i,j,k)|(0<=i,j<n
& 0<k<n).(i,(j+1) mod n,k-1)
(i,j,k)|(0<=i,j<n
& 0<k<n).(i,(j+1) mod n,k-1)
upleft =  (i,j,k)|(0<=i,j<n
& 0<k<n).((i+1) mod n,(j+1) mod n,k-1)
(i,j,k)|(0<=i,j<n
& 0<k<n).((i+1) mod n,(j+1) mod n,k-1)
prod =  (a;b).(a*b)
(a;b).(a*b)
diag =  (i,j,k)|(0<=i,j,k<=n
& i=j)
(i,j,k)|(0<=i,j,k<=n
& i=j)
Ce programme fait apparaître des routages de la forme X
= X0 /&/ (X  g o f') qui
peuvent se réécrire sous la forme : h
:: X = (h :: X0) /&/ ((h :: X)
g o f') qui
peuvent se réécrire sous la forme : h
:: X = (h :: X0) /&/ ((h :: X)  f').
f').
En effet, on peut décomposer les fonctions left et upleft de
la façon suivante :
| left = |
 (i,j,k)|(0<=k<n).(i,(j+1)
mod n,k) o (i,j,k)|(0<=k<n).(i,(j+1)
mod n,k) o |
|
 (i,j,k)|(0<k<n
& 0<=i,j<n).(i,j,k-1) (i,j,k)|(0<k<n
& 0<=i,j<n).(i,j,k-1) |
| = |
g o prev |
| upleft = |
 (i,j,k)|(0<=k<n).(i,(j+1)
mod n,k) o (i,j,k)|(0<=k<n).(i,(j+1)
mod n,k) o |
|
 (i,j,k)|(0<=i,j<n).((i+1)
mod n,j,k) o (i,j,k)|(0<=i,j<n).((i+1)
mod n,j,k) o |
|
 (i,j,k)|(0<=i,j<n
& 0<k<n).(i,j,k-1) (i,j,k)|(0<=i,j<n
& 0<k<n).(i,j,k-1) |
| = |
g o up o prev |
On peut alors procéder aux transformations :
A = A0 /&/ (A  left)
left) |
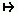 h :: A = (h :: A0) /&/ ((h :: A)
h :: A = (h :: A0) /&/ ((h :: A)  prev)
prev) |
B = B0 /&/ (B  upleft)
upleft) |
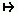 h :: B = (h :: B0) /&/ ((h :: B)
h :: B = (h :: B0) /&/ ((h :: B)  up o prev)
up o prev) |
avec h =  (i,j,k)|(0<=k<n).(i,(j+k)
mod n,k)
(i,j,k)|(0<=k<n).(i,(j+k)
mod n,k)
On doit ensuite exprimer les champs M
et V, qui dépendent de A0
et B0 en fonction de h
:: A0 et h :: B0, soit :
| M = (aligna o h-1 o h)
:: A0 |
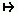 M = aligna o h-1 :: (h :: A0)
M = aligna o h-1 :: (h :: A0) |
| V = (alignb o h-1 o h)
:: B0 |
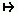 V = alignb o h-1 :: (h :: B0)
V = alignb o h-1 :: (h :: B0) |
On montre par le calcul que aligna o h-1
= aligna et alignb o h-1
= alignb.
Enfin, il faut introduire h :: A
et h :: B dans l'équation
définissant, ce qui donne, après transformations :
P = prod 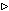 ((A /&/ B)
((A /&/ B)  diag) diag) |
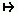 h :: P = prod
h :: P = prod 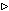 (((h :: A)
/&/ (h :: B)) (((h :: A)
/&/ (h :: B))  diag') diag') |
avec diag' = h o diag o h-1
=  (i,j,k)|(i=(j-k)
mod n)
(i,j,k)|(i=(j-k)
mod n)
On obtient ainsi le programme Matvect1'
:
Matvect1' : (M,V) 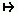 P
P
 |
h :: A0 = cube :: (h
:: A0)
h :: B0 = cube :: (h ::
B0)
M = aligna :: (h :: A0)
V = alignb :: (h :: B0)
h :: A = h :: A0 /&/
((h :: A)  prev) prev)
h :: B = h :: B0 /&/
((h :: B)  up
o prev) up
o prev)
h :: P = prod 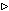 (((h :: A) /&/ (h :: B))
(((h :: A) /&/ (h :: B))  diag')
diag') |
| cube |
=  (i,j,k)|(0<=i,j,k<n).(i,j,k) (i,j,k)|(0<=i,j,k<n).(i,j,k) |
| prev |
=  (i,j,k)|(0<=i,j<n
& 0<k<n).(i,j,k-1) (i,j,k)|(0<=i,j<n
& 0<k<n).(i,j,k-1) |
| up |
=  (i,j,k)|(0<=i,j<n).((i+1)
mod n,j,k) (i,j,k)|(0<=i,j<n).((i+1)
mod n,j,k) |
| aligna |
=  (i,j,k)|(0<=i,j<n
& k=0).(i,j) (i,j,k)|(0<=i,j<n
& k=0).(i,j) |
| alignb |
=  (i,j,k)|(0<=i,j<n
& i=j & k=0).(i) (i,j,k)|(0<=i,j<n
& i=j & k=0).(i) |
| prod |
=  (a;b).(a*b) (a;b).(a*b) |
| diag' |
=  (i,j,k)|(i=(j-k)
mod n) (i,j,k)|(i=(j-k)
mod n) |
Ce programme peut encore être raffiné et mener au programme
Matvect2 :
Matvect2 : (M,V)  P
P
 |
M = aligna :: A0
V = alignb :: B0
A = A0 /&/ (A  prev)
prev)
B = B0 /&/ (B  up o prev)
up o prev)
P = prod 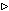 (A /&/ B)
(A /&/ B)  diag' diag' |
| prev |
=  (i,j,k)|(0<=i,j<n
& 0<k<n).(i,j,k-1) (i,j,k)|(0<=i,j<n
& 0<k<n).(i,j,k-1) |
| up |
=  (i,j,k)|(0<=i,j<n).((i+1)
mod n,j,k) (i,j,k)|(0<=i,j<n).((i+1)
mod n,j,k) |
| aligna |
=  (i,j,k)|(0<=i,j<n
& k=0).(i,j) (i,j,k)|(0<=i,j<n
& k=0).(i,j) |
| alignb |
=  (i,j,k)|(0<=i,j<n
& i=j & k=0).(i) (i,j,k)|(0<=i,j<n
& i=j & k=0).(i) |
| prod |
=  (a;b).(a*b) (a;b).(a*b) |
| diag' |
=  (i,j,k)|(i=(j-k)
mod n) (i,j,k)|(i=(j-k)
mod n) |

Exemple 13 : Introduction
d'une diffusion - application au produit matrice-vecteur
Le programme Matvect2 obtenu à l'exemple 12 peut, par introduction
d'une diffusion, raffiner le programme Matvect3 ci-dessous, utilisant uniquement
des routages de type diffusion.
Matvect3 : (M,V) 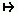 P
P
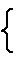 |
M = aligna :: A0
V = alignb :: B0
A = A0  spreada
spreada
B = B0  spreadb
spreadb
P = prod 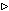 ((A /&/ B)
((A /&/ B)  diag') diag') |
| spreada |
=  (i,j,k)|(0<=i,j,k<n).(i,j,0) (i,j,k)|(0<=i,j,k<n).(i,j,0) |
| spreadb |
=  (i,j,k)|(0<=i,j,k<n).((i+k)
mod n,j,0) (i,j,k)|(0<=i,j,k<n).((i+k)
mod n,j,0) |
| aligna |
=  (i,j,k)|(0<=i,j<n
& k=0).(i,j) (i,j,k)|(0<=i,j<n
& k=0).(i,j) |
| alignb |
=  (i,j,k)|(0<=i,j<n
& i=j & k=0).(i) (i,j,k)|(0<=i,j<n
& i=j & k=0).(i) |
| prod |
=  (a;b).(a*b) (a;b).(a*b) |
| diag' |
=  (i,j,k)|(i=(j-k)
mod n) (i,j,k)|(i=(j-k)
mod n) |

Exemple 14 : Cadencement
des équations récurrentes - processus de diffusion discrète
Le processus de diffusion discrète s'écrit ainsi :
do i = 1,n
do j = 1,n
y(i,j) = f(y(i-1,j),y(i,j-1))
enddo
enddo
ce qui, en PEI, s'écrit de la façon
suivante :
Y = f 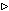 (X /&/ (Y
(X /&/ (Y  f1) /&/ (Y
f1) /&/ (Y  f2))
f2))
f1 =  (i,j)|(1<=i,j<=n).(i-1,j)
(i,j)|(1<=i,j<=n).(i-1,j)
f2 =  (i,j)|(1<=i,j<=n).(i,j-1)
(i,j)|(1<=i,j<=n).(i,j-1)
où X est le champ contenant
les valeurs initiales. Il existe, pour ce type de problème, une
transformation affine temps x espace permettant de paralléliser
la récurrence. Ici, cette transformation peut être :
| ( |
t
p |
) = ( |
1 1
1 0 |
) ( |
i
j |
) |
où l'indice t représente le temps et p les processeurs. En
PEI, cette transformation est réalisée
en effectuant le changement de base h
=  (t,p).(t+p,t). On
peut donc raffiner le programme précédent et obtenir :
(t,p).(t+p,t). On
peut donc raffiner le programme précédent et obtenir :
Y' = f 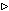 (X' /&/ (Y'
(X' /&/ (Y'  g1) /&/
(Y'
g1) /&/
(Y'  g2))
g2))
g1 =  (t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p-1)
(t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p-1)
g2 =  (t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p)
(t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p)
où g1 = h o f1 o h-1
et g2 = h o f2 o h-1

Exemple 15 : Traduction
d'un changement de base en HPF
| Enoncé PEI |
Traduction en HPF |
X = matrix :: X
Y = transl :: X
transl =  (i,j)|(1<=i,j<=n).(i+1,j) (i,j)|(1<=i,j<=n).(i+1,j)
matrix =  (i,j)|(1<=i,j<=n).(i,j) (i,j)|(1<=i,j<=n).(i,j) |
type X(1:n), type Y(2:n+1)
template T(n+1,n)
align X(i,j) with T(i,j)
align Y(i,j) with T(i+1,j)
forall (i=1:n,j=1:n) Y(i+1,j) = X(i,j) |

Exemple 16 : Traduction
d'une réduction géométrique combinée avec une
opération fonctionnelle en HPF
| Enoncé PEI |
|
|
|
|
Y = sum 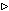 (red
; (red
;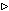 X) X)
sum = id #  (a;b).(a+sum(b)) (a;b).(a+sum(b))
red =  (i,j)|(1<=i,j<=3).(i,i) (i,j)|(1<=i,j<=3).(i,i) |
|
[ |
1 2 3
1 2 3
1 2 3 |
]) |

Exemple 17 :
Traduction d'une définition récursive en HPF
Considérons l'énoncé de l'exemple
14 :
| Enoncé PEI |
Traduction en HPF |
Y' = f  (X' /&/ (Y'
(X' /&/ (Y'  g1) /&/
(Y' g1) /&/
(Y'  g2)) g2))
g1 =  (t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p-1) (t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p-1)
g2 =  (t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p) (t,p)|(1<=p<=n
& 1<=t-p<=n).(t-1,p) |
forall
(t=1, p=0:1) Y'(t,p) = X(t,p)
do t = 2,2*n
forall (p=max(1,t-n):min(n,t-1))
& Y'(t,p) =
f(X'(t,p),Y'(t-1,p-1),Y'(t-1,p))
enddo |



Jacques-Alexandre Gerber's Home
Page - écrivez-moi!