The parametric vertices

The loop nest is modeled by the one-parameter polyhedral iteration space defined by:

P_n = { (i, j, k) in Z^3 | 0 <= i <= n, 0 <= j <= i, 0 <= k <= i-j }

From a geometrical point of view, all the points (i, j, k) of P_n resulting in the same value of t = t(i, j, k), belong to the two-parameters rational polytope:

T_{n, t} = P_n × { (i, j, k) in Z^3 | i + j + k = t }

The number of points in T_{n, t} is par(n, t).
Giving this last parametric definition of T_{n, t} as an input to the parametric vertices finding program, it outputs the following results:

if 0 <= t <= n, the parametric vertices are v1 = (t, 0, 0), v2 = (t/2, t/2, 0), v3 = (t/2, 0, t/2) (Figure 1).
if n <= t <= 2n, the parametric vertices are v2 = (t/2, t/2, 0), v3 = (t/2, 0, t/2), v4 = (n, t - n, 0), v5 = (n, 0, t-n) (Figure 2).
otherwise, T_{n, t} does not exist and par(n, t) = 0.


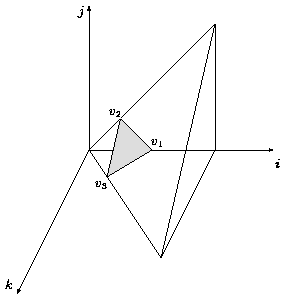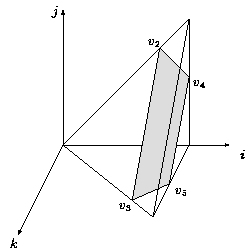Figure 1	Figure 2

Previous page: Problem description
Next page: Ehrhart polynomials and maximum parallelism

The parametric vertices

Figure 1

Figure 2