Notions abordées : parcours d'un graphe, recherche d'un chemin.
On considère ici des graphes orientés simples finis et
l'on souhaite trouver la liste des sommets du graphe dans l'ordre du
parcours en profondeur. Réutiliser les opérations de base définies dans le
TP précédent pour définir une fonction parcours_prof(g,x)
dont le résultat est cette liste en partant du sommet x (la
définition de cette fonction doit être indépendante de la représentation
du graphe : matrice ou listes d'adjacence). Il faudra définir et utiliser
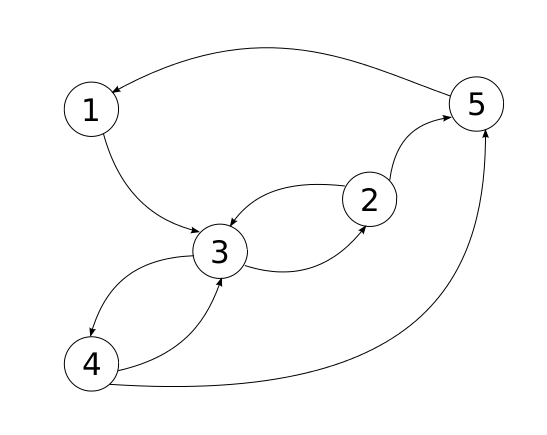
proprement le type des listes. Exemple : pour le graphe ci-dessous, on obtient
la liste 1,3,4,5,2.

(indication : cette définition en OCaml)
Même question que dans l'exercice précédent, mais avec
le parcours en largeur et la fonction parcours_largeur(g,x).
Il faudra définir et utiliser le type des files. Exemple : pour le graphe
ci-dessous, on obtient la liste 1,3,4,2,5.

Etant donné un graphe orienté simple, il s'agit de trouver un chemin (s'il
en existe un) entre deux sommets x et y.
Définir une fonction trouve_chemin(g,x,y) qui donne la liste
des sommets successifs pour passer de x à y.
On utilisera une pile dont les éléments correspondent aux étapes
sucessives sur le chemin (Il faudra donc définir au préalable le type des
piles). Utiliser cette fonction pour trouver la solution du célèbre problème de la
chèvre, du chou et du loup.
(indication : cette définition en OCaml)
On considère ici des graphes orientés dont les arcs
ont une certaine longueur et l'on souhaite savoir quel est la distance la
plus courte entre deux sommets x et y.
Représenter ce type de graphes en C (au choix par une matrice ou des
listes d'adjacence). Définir une fonction distance(g,x,y) qui donne la
distance du chemin le plus court pour passer de x à y. Utiliser l'algorithme de
Dijkstra. Tester votre fonction sur l'exemple ci-dessous (la
distance la plus courte pour aller de A à J est 487 : le chemin à suivre
passe par C et H).
