Programmation Orientée Objet

TP n° 3

Tableau, pile, arbre binaire

On désire écrire un programme Java permettant d'évaluer des expressions écrites en polonaise inversée. La notation polonaise inversée ou post-fixée permet de noter les formules arithmétiques sans utiliser de parenthèses.

Exemples :

Écriture usuelle	Écriture en polonaise inversée
(2+3)*4	2 3 + 4 * 4 2 3 + *
1 + (2 + 3)	1 2 3 + +
2 – 3	2 3 -

Pour effectuer le calcul, chaque donnée numérique est empilée, et lorsqu'on lit un opérateur, les opérandes sont dépilés (2 si l'opérateur est binaire), l'opération est effectuée et le résultat est mis au sommet de la pile.
Ainsi, par exemple, pour évaluer 2 3 + 4 * :

1. lecture de 2 qui est reconnu comme donnée numérique et de ce fait est empilé,

2. lecture de 3 qui est également empilé,

3. lecture de + qui est un opérateur binaire : 2 et 3 sont dépilés, le calcul 2 + 3 est effectué, le résultat 5 est empilé,

4. lecture de 4 qui est empilé,

5. lecture de * , opérateur binaire : 4 et 5 sont dépilés, le calcul 4*5 est effectué et le résultat 20 est empilé,

6. la chaîne est entièrement lue → le résultat final est au sommet de la pile.

Dans votre programme Java, la pile sera à base d'un tableau et ses éléments de type Integer.

Écrire la classe PileParTableau qui comporte :

comme attributs :

• Integer tab[] : la pile

• int indice qui mémorise une position dans le tableau ; c'est l'emplacement du premier élément non utilisé.

Note : la taille du tableau n'est pas mémorisée étant donné qu'elle peut être calculée (tab.length).

comme constructeur

• PileParTableau(int) : l'argument est la taille de la pile (du tableau) à allouer.

et les méthodes spécifiques aux piles :

• boolean pileVide() qui renvoie true si la pile est vide et false sinon.

• boolean pilePleine() qui renvoie true si la pile est pleine, et false sinon.

• Integer depiler() qui renvoie l'objet au sommet de la pile (à condition que la pile ne soit pas vide)

• void empiler(Integer) qui copie l'entier transmis en argument au sommet de la pile (à condition que la pile ne soit pas déjà pleine).

On ne demande aucune gestion particulière des erreurs. Renvoyer null si la pile à dépiler est vide et ne rien faire s'il faut empiler un nouvel élément dans une pile pleine.

Écrire ensuite la classe Expression. Cette classe comporte :

• un attribut line de type String qui comporte une expression en polonaise inversée,

• un constructeur Expression(String) qui permet d'initialiser l'attribut line,

• Integer evalue() qui évalue l'expression. Il faut

• Extraire de line les différentes sous-chaînes correspondant aux opérandes et opérateurs. Pour ce faire, utiliser la méthode split qui est une méthode d'instance de la classe String définie comme suit :

public String[] split(String regex)

Cette méthode a déjà été utilisée lors d'un précédent TP.

• Instancier un objet de type PileParTableau pour effectuer votre calcul.

• Lire les opérandes et opérateurs et effectuer les opérations correspondantes.

Vous pouvez compléter votre classe avec des méthodes privées telles que :

• private boolean operateur(String) ; qui renvoie true si la chaîne transmise en argument correspond à un opérateur "reconnu " et false sinon ;

• private void calcul(PileParTableau, char) qui a comme arguments la pile avec laquelle effectuer le calcul et l'opérateur. Dans cette méthode, les opérandes sont dépilés, l'opération effectuée et le résultat est stocké au sommet de la pile.

Écrire la classe TestPile qui comporte la méthode main où s'effectue la lecture interactive de l'expression polonaise à calculer et l'affichage du résultat.

Exercice 2. Arbre binaire

Reprendre l'exercice sur les arbres binaires vu en TD.

Tester les méthodes déjà programmées.

Finir l'exercice.

Indications pour la suppression d'un nœud :

1. Le nœud à supprimer est feuille de l'arbre

• rechercher son père,

• mettre le pointeur du père qui fait référence à ce nœud à null (fils gauche ou fils droit suivant le cas).

2. Le nœud à supprimer n'est pas feuille (nœud interne ou racine de l'arbre)

• le nœud à supprimer a un sous-arbre gauche : le remplacer par son prédécesseur qui est la plus grande clé de son sous-arbre gauche. Pour ce faire :

• chercher la valeur du prédécesseur,

• supprimer cette feuille (appel récursif),

• mise à jour du champ "donnée" du nœud à supprimer avec la valeur de son prédécesseur ;

• si le nœud à supprimer n'a pas de sous-arbre gauche, il aura un sous-arbre droit. Remplacer alors le nœud par son successeur qui est la plus petite clé de son sous-arbre droit. Pour ce faire,

• chercher la valeur du successeur,

• supprimer cette feuille (appel récursif),

• mise à jour du champ "donnée" du nœud à supprimer avec la valeur de son successeur.

Cas particulier qui posera problème : l'arbre est constitué d'un seul nœud qui est le nœud à supprimer.

Exemple

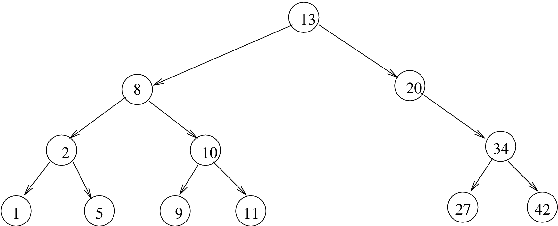
Soit l'arbre binaire avec des données entières :

• suppression du nœud dont la valeur est 11 (feuille) : il est fils droit de son père. Son père, nœud de valeur 10 n'aura plus de fils droit ;

• suppression de 8 : prédécesseur = 5 ; suppression de la feuille ayant pour valeur 5, remplacement dans l'arbre du 8 par 5 ;

• suppression de 20 : successeur = 27 ; suppression de la feuille ayant pour valeur 27, remplacement du 20 par 27.