Programmation Fonctionnelle
(sujet
n°2)
I. Définition de types algébriques et filtrage.
(a) Taper la définition du type des cartes à jouer (vu en cours)



(d) Ecrire une fonction qui détermine si un paquet donné contient les 4 as.
II. Types classiques.
1. Listes
(d) Le problème des Tours de Hanoï est un problème classique. Il peut être résolu de manière très élégante en utilisant les listes. Ecrire en quelques lignes une fonction
2. Arbres binaires
(a) Définir le type tree des arbres binaires polymorphes avec une valeur à chaque noeud (branche ou feuille).
(b) Donner l'expression Ocaml de l'arbre suivant: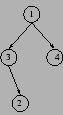
3. (Question facultative) Arbres binaires de recherche
Un arbre binaire de recherche est un arbre binaire vérifiant : en tout noeud, la valeur x en ce noeud, est strictement les valeurs dans le sous-arbre gauche sont strictement inférieures à x et les valeurs dans le sous-arbre droit sont strictement supérieures.
(b) Ecrire une fonction add qui ajoute une valeur à un arbre binaire de recherche (en supposant que la valeur n'est pas déja dans l'arbre).
(c) Ecrire une fonction remove_max prenant pour argument un arbre binaire de recherche non vide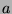 ,
et qui retourne le couple
,
et qui retourne le couple 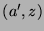 où
où 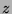 est la
plus grande valeur apparaissant dans
est la
plus grande valeur apparaissant dans 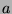 , et
, et 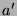 est
l'arbre obtenu à partir de
est
l'arbre obtenu à partir de 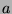 en
retirant le noeud valué par
en
retirant le noeud valué par 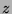 .
.
(d) En déduire une fonction remove qui supprime une valeur d'un arbre binaire de recherche.
[Page réalisée par Eric Violard]
I. Définition de types algébriques et filtrage.
(a) Taper la définition du type des cartes à jouer (vu en cours)
(b) En s'inspirant de la
définition du type des listes, définir un type
paquet_de_carte
à l'aide de 2 constructeurs: Derniere (qui
construit un paquet avec une seule carte) et Dessus (qui
construit un paquet en ajoutant une carte au-dessus d'un paquet).(c) Donner une expression Ocaml
correspondant à un paquet de carte composé d'un as de
coeur, d'un roi de tréfle et d'un 10 de carreau.



(d) Ecrire une fonction qui détermine si un paquet donné contient les 4 as.
(e) Ecrire une fonction qui trie un
paquet de cartes par couleur dans l'ordre suivant : d'abord les coeurs
(au-dessus), puis les carreaux, puis les piques et enfin les
trèfles (à la fin du paquet).
(f) (Question facultative) Ecrire une
fonction qui étant donné 2 paquets de cartes
détermine lequel est gagnant au jeu
de la bataille.
II. Types classiques.
1. Listes
(a) Rédéfinir et
expérimenter les fonctions suivantes sur les listes polymorphes
(le nom de la fonction prédéfinie est donné en
gras) :
longueur(longueur d'une liste)List.lengthtete(premier élément d'une liste)List.hdreste(la liste sans son premier élément)List.tlnieme(n-ième élément d'une liste : les éléments sont numérotés à partir de 0)List.nthinverse(liste obtenue en renversant une liste : le 1er élément devient le dernier, le 2ème devient l'avant-dernier, ...)List.revconcat(concaténation de 2 listes)List.appendou(@)
(b) On choisit de noter un ensemble
(en extension) par une liste. Ex. [1;2;5] note l'ensemble des entiers
1, 2 et 5. On peut remarquer qu'il y a plusieurs notations pour le
même ensemble. Ex. les listes [1;2;5], [1;5;2] ou [5;1;2] notent
le même ensemble. De plus, on convient qu'un même
élément dans un ensemble peut apparaître plusieurs
fois dans la liste correspondante. Ex. [1;2;2;5], [1;1;2;5] ou encore
[2;1;5;2;5] désigne le même ensemble. Ecrire les fonctions
suivantes sur les ensembles :
union(union de 2 ensembles)intersection(intersection de 2 ensembles)inclus(test d'inclusion d'un ensemble dans un autre)difference(différence de 2 ensembles : les éléments du premier ensemble sans les éléments du second)egal(test d'égalité de 2 ensemble)
permut
qui étant donné un ensemble donné par une liste
sans doublon, détermine la liste de toutes les autres listes
sans doublon qui désignent le même ensemble (autrement dit
la liste de toutes les permutations des éléments d'une
liste). Ex. permut [1;2;3];; donne
[[1;2;3];[1;3;2];[2;1;3];[2;3;1];[3;1;2];[3;2;1]].(d) Le problème des Tours de Hanoï est un problème classique. Il peut être résolu de manière très élégante en utilisant les listes. Ecrire en quelques lignes une fonction
deplacer qui retourne la
liste des déplacements à effectuer pour faire passer n
disques de l'emplacement de vers l'emplacement a
en passant par l'emplacement intermédiaire par,
étant donné le quadruplet (n, de, a,
par). Ex. Liste des déplacements de
3 disques de l'emplacement 1 à l'emplacement 3 en passant par
l'emplacement 2 :
# deplacer (3,1,3,2);;
- : (int * int) list =
[(1, 3); (1, 2); (3, 2); (1, 3); (2, 1); (2, 3); (1, 3)]2. Arbres binaires
(a) Définir le type tree des arbres binaires polymorphes avec une valeur à chaque noeud (branche ou feuille).
(b) Donner l'expression Ocaml de l'arbre suivant:

(c) Définir une fonction size
qui calcule le nombre de ses noeuds
(d) Définir une fonction height
qui calcule la hauteur d'un arbre. On appelle hauteur d'un
arbre la longueur maximale d'un chemin direct de la racine à un
noeud quelconque.
(e) Définir une fonction max_tree qui calcule la plus grande valeur présente dans un arbre.
(e) Définir une fonction max_tree qui calcule la plus grande valeur présente dans un arbre.
3. (Question facultative) Arbres binaires de recherche
Un arbre binaire de recherche est un arbre binaire vérifiant : en tout noeud, la valeur x en ce noeud, est strictement les valeurs dans le sous-arbre gauche sont strictement inférieures à x et les valeurs dans le sous-arbre droit sont strictement supérieures.
(a) Ecrire une fonction mem qui teste si une valeur donnée apparaît dans un arbre de recherche donné.
(b) Ecrire une fonction add qui ajoute une valeur à un arbre binaire de recherche (en supposant que la valeur n'est pas déja dans l'arbre).
(c) Ecrire une fonction remove_max prenant pour argument un arbre binaire de recherche non vide
(d) En déduire une fonction remove qui supprime une valeur d'un arbre binaire de recherche.
[Page réalisée par Eric Violard]